
AAA robot giocoliere cercasi
Se culturalmente ed artisticamente il juggling in Occidente veniva progresivamente degradato a fenomeno da baraccone, in ambienti scientifici l’interesse per i giochi di destrezza non ha tardato a manifestarsi. Lo studio dell'abilità nel praticare il juggling, oltre a chiarire vari aspetti della coordinazione umana, ha infatti trovato interessanti applicazioni in robotica e matematica. Con questa rubrica cercheremo di curiosare nei prestigiosi laboratori di ricerca scientifica dove ai robot viene concesso in tenera età di divertirsi giocando con palline e clavette, prima di essere spediti in fabbrica a saldare le scocche delle automobili........
Il primo studio scientifico conosciuto risale al 1903, quando Edgar James Swift pubblicÚ un articolo sull' "American Journal of Psycology" nel quale forniva dati sulla velocità con cui alcuni studenti imparavano a lanciare in aria due palle con una mano. Negli anni '40 si inizio' ad utilizzare il calcolatore per studiare le traiettorie di oggetti lanciati, e venne fondata la International Jugglers Association. Gli anni '50 e '60 videro poche e saltuarie applicazioni, soprattutto ad opera di seguaci di Swift che sfruttavano i giochi di destrezza per valutare l'apprendimento di abilità sensomotorie. Infine, negli anni '70, i giochi di destrezza iniziarono ad essere studiati per se stessi. Al MIT, Claude E. Shannon invento' macchine giocoliere e formulo' il teorema di destrezza, in cui si esprime la relazione tra posizione delle palle e azione delle mani. Seymour A. Papert e altri ricercatori del progetto MIT (che in seguito divenne l'Artificial Intelligence Laboratory del MIT) studiarono il modo in cui si impara a padroneggaire l'arte della giocoleria, e venne fondato il club dei giocolieri del MIT. Negli anni '80 nacque la matematica del gioco di destrezza. e diversi studiosi elaborarono un particolare tipo di notazione per indicare gli esercizi .
Le ovvie restrizioni fisiche che limitano le possibilità di controllo e il numero di oggetti lanciati derivano dalla gravità, e più specificatamente dalla meccanica newtoniana. Ciascuna palla deve essere lanciata abbastanza in alto da dare al giocoliere il tempo per manovrare le altre. Il tempo che una palla trascorre in aria é proporzionale alla radice quadrata dell'altezza del lancio. La velocit‡ o l'altezza richieste crescono rapidamente con il numero di oggetti lanciati. Il modo in cui i giocolieri, all'interno di questi vincoli, riescono a coordinare gli arti ritmicamente e alla stessa frequenza È diventato un argomento di primaria importanza nello studio del movimento umano. I ricercatori impegnati in questo settore hanno mutuato da queste acrobazie alcuni concetti dalla teoria matematica degli oscillatori accoppiati.
Il fenomeno chiave dell'oscillazione accoppiata È la sincronizzazione: la tendenza di due arti a muoversi alla stessa frequenza. Il particolare tipo di coordinazione mostrato dalle mani che eseguono un gioco di destrezza dipende dal tipo di esercizio. In linea teorica si puo' eseguire la fontana con frequenze diverse per le due mani, ma in questo caso la coordinazione é resa difficile dalla tendenza degli arti a muoversi in sincronia.
Le variabili associate al lancio (angolo di uscita, velocità di uscita, localizzazione e altezza dei lanci) sono le più controllabili: i giocolieri cercano di lanciare le palle nel modo più uniforme possibile, secondo una distribuzione temporale che deve obbedire al teorema di Shannon. Data una certa altezza del lancio, una misura cruciale della velocità d'esecuzione é il cosiddetto "rapporto di pausa", ossia la frazione di tempo durante la quale la mano trattiene una palla tra due prese (o due lanci). Lanciare e riprendere tre oggetti lascia ampie possibilità di modificazioni, adattamenti, trovate e abbellimenti; invece non ci sono molti modi per eseguire un esercizio con nove oggetti.
Costruire modelli di questi schemi di movimento, pero', dice poco sulla necessaria coordinazione mano-occhio. I giocolieri devono ricevere informazioni sui movimenti sia delle mani sia delle palle. L'attenzione deve passare da una palla alla successiva, e quindi il giocoliere vede solo una parte della traiettoria di ciascuna palla. Quale parte della traiettoria trasmette più informazioni e richiede maggiore attenzione visiva? Esperimenti condotti al MIT nel 1974 dimostrarono che si poteva riuscire in una presa anche quando rimanevano visibili solo due centimetri e mezzo della traiettoria in corrispondenza del punto più alto raggiunto dalla palla. Dato che questo corrisponde a un tempo di visione di circa 50 millisecondi, ne segue che é sufficiente una rapida occhiata al culmine della traiettoria per la riuscita dell'esercizio. Sorpresi!!?
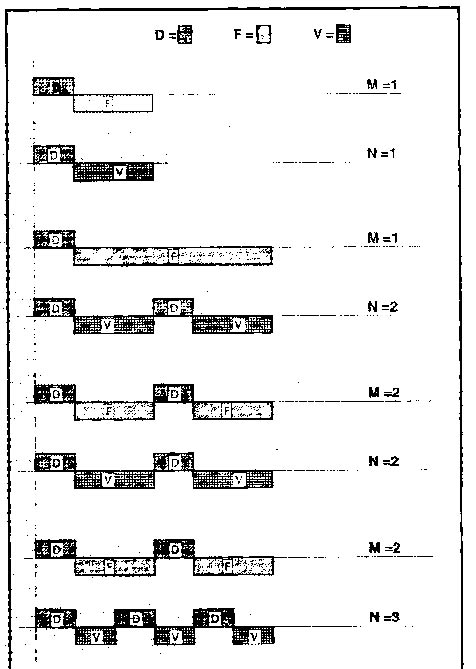
equazione di Shannon:
(F+D) x M = (V+D) x N
D = tempo della palla in mano
F = tempo della palla in aria
V = tempo in cui la mano é vuota
M = numero delle mani
N = numero delle palle
Hp: D (tempo della palla in mano) = 3 sec.
Hp: F (tempo della palla in aria) = 6 sec.
Hp: quando si usano una palla e una mano, l’eqazione si riduce a F = V



